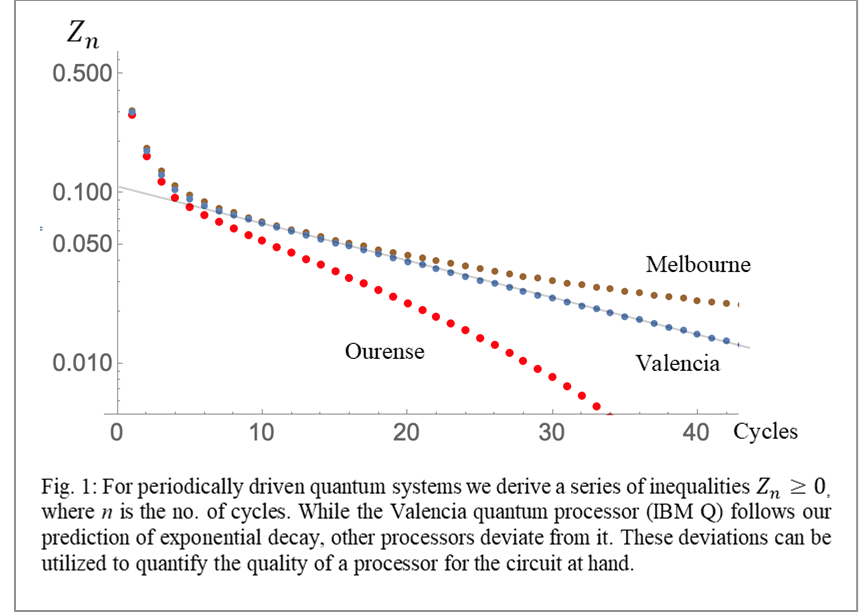
We derive a set of inequalities on the evolution of the survival probability in periodically driven quantum systems. By repeating the same circuit multiple times, we can detect 1) violation from perfect periodicity (e.g. due to a systematic drift in the controls). 2) Heat leaks that make the evolution non-unital. To obtain these inequalities we introduce the principle of “positivity” in Liouville space. Crucially, we can detect heat leak in scenarios that are impossible to detect by measuring observables after just one cycle (e.g. when the initial is at zero temperature). Generally, our method works very well for pure-states initial condition and therefore it is suitable for NISQ quantum processors. We verify our findings experimentally on the IBM Q platform.
Our second main finding is that these inequalities exponentially converge to equality as the number of cycles increases. The exponential decay is universal in the sense that it appears for any circuit and for any initial condition provided that the driving is periodic. The decay rate is directly related to the “action” of the circuit. A deviation from exponential decay can be used as an indicator of the imperfection of the device at hand. We will present results from the IBM Q and discuss the potential of this method to diagnose problems in realizations of quantum circuits.